
Dans son cadre le plus général, l'optimisation d'une fonction permet de rechercher l'ensemble de paramètres permettant d'obtenir le meilleur résultat. Je m'intéresserai uniquement aux fonctions à paramètres et à valeurs réelles. Nous avons donc deux approches duales : la maximisation et la minimisation. Je vais présenter ici des techniques de minimisation; la maximisation d'une fonction f se ramène à la minimisation de la fonction -f .
La recherche du minimum peut être faite de façon analytique, ou de façon numérique. Dans la grande majorité des cas réels, la fonction à optimiser n'est pas minimisable de façon analytique. On recourt donc à des méthodes numériques, et plus particulièrement l'échantillonnage et la descente de gradient. La première de ces méthodes consiste à évaluer la valeur de la fonction pour chacun des jeux de paramètres possibles. La seconde se base sur l'amélioration d'une solution approchée.
La minimisation par échantillonnage (on dit aussi par balayage) assure que le minimum de la fonction sera trouvé. De plus, la recherche est faite en un temps constant, qui ne dépend que du nombre de jeux de paramètres à tester. La minimisation par descente de gradient permet quant à elle de ne pas tester tous les jeux de paramètres. L'amélioration progressive d'une solution partielle permet en effet de concentrer ses efforts aux environs de la solution recherchée. Néanmoins, cette seconde approche se heurte aux problèmes des minima locaux. En effet, rien ne garantit qu'il n'existe pas d'autre minimum local, ni que sa valeur soit supérieure à celle du minimum trouvé.
Afin de minimiser une fonction à partir d'une solution approchée, le plus simple est de suivre la ligne de plus grande pente. D'un point de vue mathématique, la pente d'une fonction correspond à la dérivée de cette dernière. Si l'on se place dans le cadre d'une fonction ayant plusieurs paramètres, la dérivée devient un vecteur : le gradient de la fonction. Chaque élément de ce vecteur correspond alors à la dérivée partielle de la fonction selon l'un de ses paramètres.
J'ai déjà exprimé la limite la plus importante de cette méthode d'optimisation : le problème des minima locaux. En effet, même si l'on considère un cas simple, comme celui de la figure suivante, il arrive fréquemment que le minimum global soit masqué par un maximum, local lui aussi. Dans cet exemple, en partant du point marqué d'une croix, il est impossible d'aller au-delà du point marqué d'un cercle. En effet, toute variation du paramètre implique une augmentation de la valeur, et donc une dégradation de la solution.

La seconde limite de cette méthode tient à la notion de paramètre borné. En effet, il arrive souvent que certains paramètres ne soient valides que dans un certain intervalle. Par exemple, dans le cadre d'un modèle probabiliste, une probabilité ne peut pas être négative, et ne doit pas dépasser 100%. Or la descente de gradient peut amener à dépasser ces limites si l'on n'y prend pas garde. Ainsi, l'image ci-dessus montre une pente importante au niveau de la borne inférieure. Elle semble donc indiquer la présence d'un minimum intéressant en dessous de cette borne. Il faut donc ajouter aux algorithmes classiques des gardes permettant de garantir la validité des paramètres.
Finalement, afin de suivre la ligne de plus grande pente, il est nécessaire d'évaluer cette pente. Si la fonction à optimiser est dérivable, il suffit de calculer sa dérivée au niveau de la solution approchée. Cependant, toutes les fonctions ne sont pas dérivables. En particulier, il peut être intéressant d'optimiser des fonctions dont la formule analytique est inconnue. Par exemple, la fonction pourrait être calculée par un dispositif expérimental. Alternativement, la dérivée de la fonction que l'on cherche à minimiser peut simplement être trop compliquée à calculer, ou même ne pas exister du tout.
La minimisation par encadrements successifs est une approche voisine de la descente de gradient. Cette nouvelle méthode essaye en effet d'améliorer une solution approchée, mais sans calculer de pente. A la place, on utilise une évaluation de la fonction de part et d'autre de la solution approchée. Si la nouvelle valeur est inférieure, nous avons amélioré la solution.
L'avantage principal de cette méthode est qu'elle se prête naturellement à l'optimisation de fonction non dérivables à paramètres bornés. En effet, la dérivée de la fonction n'est nécessaire à aucun moment. De plus, le choix des valeurs encadrant la solution est tel qu'il est impossible d'enfreindre les limites de validité des paramètres. L'inconvénient majeur de cette approche est qu'il lui est impossible d'optimiser une fonction ayant plusieurs paramètres. Pour palier ce défaut, il est possible de mettre en oeuvre des méthodes dites de relaxation.
Afin d'expliquer cet algorithme, je vais m'intéresser tout d'abord au cas unidimensionnel, en me basant sur la figure suivante :

Les points A et B correspondent aux bornes de validité du paramètre, et le point C correspond à la solution approchée actuelle. Pour améliorer cette solution, on va choisir un point de part et d'autre de C :

La fonction ayant sa valeur minimale en E, nous avons déjà trouvé une meilleure approximation de la solution. En admettant que la fonction est relativement régulière, on peut supposer que, si une meilleure approximation existe, elle se trouvera soit entre C et E, soit entre E et B. On peut donc éliminer l'intervalle situé entre A et C. Pour se ramener à la situation précédente, renommons C et E en A et C. On va donc choisir un point de part et d'autre de notre nouveau point C :
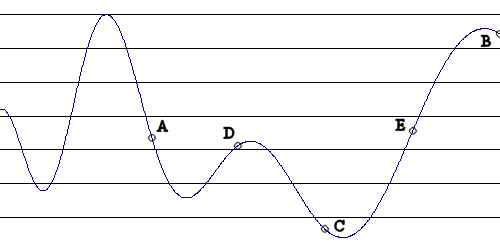
La fonction ayant toujours sa valeur minimale en C, nous pouvons éliminer les intervalles situés entre A et D, et entre E et B. On se ramène alors à la situation précédente. En répétant le processus, on voit donc que l'on peut réduire l'intervalle de recherche très rapidement. Ce processus s'arrêtera naturellement lorsque l'intervalle situé entre A et B sera suffisamment petit.
Cependant, il existe un cas particulier ennuyeux : lorsque le minimum se trouve sur l'une des bornes de l'intervalle de validité. On se limite alors à une recherche asymétrique, en ne réduisant l'intervalle que dans la zone de validité.
Cette minimisation est donc une recherche dichotomique du minimum de la fonction. D'autre variantes sont possibles, selon la manière de choisir les nouveaux points. L'excellent livre Numerical Recipes (en anglais) présente ces diverses méthodes en détail.
Voici une applet Java (1.4) permettant de mettre en oeuvre la minimisation d'une fonction par encadrement. Vous pouvez évaluer la fonction (cachée) en un point en cliquant à la souris à cet endroit. Essayez de trouver le minimum en aussi peu de clicks que possible, et vérifiez en cliquant sur Balayage.
Accès au code sourceLes méthodes de relaxation permettent d'optimiser des fonctions ayant plusieurs arguments, tout en n'utilisant que des optimisations de paramètres seuls. Il est donc nécessaire de s'intéresser à elles avant de pouvoir appliquer, entre autres, l'algorithme présenté ci-dessus à des cas réels. Je vais donc tout d'abord présenter la méthode de relaxation standard, puis celle de Powell. J'exposerai finalement la méthode que je propose pour l'optimisation de modèles probabilistes.
La méthode de relaxation la plus classique repose sur l'optimisation de chacun des paramètres tour à tour. En effet, en raisonnant par l'absurde, on peut montrer que le fait d'avoir une fonction optimale pour chacun de ses paramètres est une condition nécessaire à l'obtention d'un optimum de la fonction. Ainsi, supposons que la fonction f dispose d'un jeu de n paramètres { Pi }. A l'optimum, Pi = vi, la fonction a une valeur V*.
Supposons maintenant que l'un des paramètres, P0 par exemple, ne soit pas optimal pour la projection de f sur P0 : il existe une valeur w0 telle que la valeur de la projection de f sur P0 soit meilleure que celle obtenue en v0. On aura donc f ( w0, v1..n ) qui sera meilleure que V*. L'ensemble de paramètres { vi } n'est donc pas optimal pour f.
On peut donc garantir que, si la fonction est simultanément optimale pour chacun des paramètres, l'ensemble des valeurs de ces paramètres forme un optimum local de la fonction. Malheureusement, on ne peut pas en déduire que, si l'optimum est global pour chacun des paramètres, il sera aussi global pour la fonction. Il ne reste donc qu'à optimiser la fonction séparément sur chacun de ses paramètres pour obtenir un optimum de la fonction. Cependant, il est bon de noter que les paramètres ont rarement des effets indépendants. L'optimisation d'un paramètre va donc modifier la valeur de la fonction projetée sur les autres, et donc fausser un optimum calculé auparavant.
L'algorithme de relaxation est donc le suivant :
La méthode de relaxation standard fonctionne relativement bien, mais elle est très inefficace. En effet, dans certains cas, chaque pas amène à une petite optimisation, qui permet une petite optimisation d'un autre paramètre, et ainsi de suite. Par exemple, l'image suivante reflète un tel cas :


La solution initiale se trouve en haut et à gauche de l'image, et la première optimisation se fait selon l'axe des abscisses. La seconde sera selon l'axe des ordonnées, puis on itère le processus jusqu'à arriver au minimum. Voici les coupes de cette fonction pour les trois premières étapes :

Première étape

Deuxième étape

Troisième étape
Afin de pallier cette lenteur, Powell a proposé une méthode de relaxation originale : son idée est d'effectuer une descente directement le long de la ligne de plus grande pente, et non selon les axes. Afin d'approcher cette direction, sans calculer le gradient de la fonction, il se base sur la conjuguée des précédentes optimisations. Ainsi, en règle générale, cette résultante est orientée approximativement selon la ligne de plus grande pente. Néanmoins, comme le montre bien le premier pas de l'optimisation menée ci-dessus, il arrive que cette résultante soit complètement absurde. C'est souvent le cas lors du premier pas, et surtout si la solution initiale est loin de l'optimum. Cependant, on voit bien dans la seconde étape que la résultante est particulièrement bien orientée.
Afin de ne pas augmenter la complexité de l'optimisation, Powell propose de remplacer l'un des paramètres par cette nouvelle direction. L'idéal est de choisir le paramètre ayant la plus forte influence sur celle-ci. En effet, il est essentiel de garder des vecteurs de descentes non colinéaires afin de pouvoir parcourir l'intégralité de l'espace des paramètres. Le choix du paramètre le plus colinéaire est donc une solution avisée.
Cependant, au bout d'un certain nombre d'itérations, les risques d'obtenir au moins deux vecteurs colinéaires (ou presque colinéaires) augmentent rapidement. Brent propose donc de restaurer l'ensemble de vecteurs d'optimisation au bout d'un certain nombre d'étapes.
La relaxation de Powell permet donc, si l'on fait un peu attention, d'accélérer grandement la recherche de l'optimum. Cependant, elle ne permet pas de tenir compte des bornes de validité des paramètres pendant la descente selon une direction résultante des optimisations précédentes. J'ai donc proposé une variante de cette méthode adaptée à un jeu de paramètres probabilistes, dont les bornes sont liées.
En effet, chacune des probabilités du modèle doit s'échelonner entre 0 et 100%, ce qui correspond à la contrainte la plus classique. De plus, la somme des probabilités issues d'une même distribution doit faire 100%. Afin d'assurer la valeur de ces sommes, il faut tout d'abord retirer un paramètre par distribution. La valeur de ce paramètre sera définie automatiquement de façon à assurer la cohérence de la distribution. Ensuite, il reste à assurer que la somme des paramètres attachés à une même distribution soit inférieure à 100%.
Afin de simplifier le problème, j'ai décidé de ne pas remplacer l'un des paramètres par la direction calculée selon la méthode de Powell. J'ai simplement ajouté ce paramètre à l'ensemble existant. L'inconvénient de cette approche tient à ce qu'il est impossible de suivre plusieurs axes de descente conjuguée. En effet, à chaque cycle, la direction de descente conjuguée du cycle précédent est remplacée par la nouvelle. Il est donc probable que l'on perde un peu en vitesse de convergence. Cependant, cette approche rend le calcul des bornes des paramètres relativement simple. De plus, aucune dégénérescence du modèle n'est à craindre, puisque aucun paramètre n'est remplacé. Il n'est donc aucun besoin de régénérer cet ensemble comme le recommande Brent.
Il reste donc à calculer les bornes de ce nouveau paramètre. Formellement, supposons que
k paramètres soient issus de la même distribution. Au cours de ce cycle
d'optimisations, chaque paramètre est modifié d'un certain  . Il reste donc à définir les bornes du
paramètre
. Il reste donc à définir les bornes du
paramètre  tel que :
tel que :

On peut tout d'abord remarquer que les contraintes sont internes à chaque distribution de
probabilités. Il suffit donc de calculer les bornes imposées par chacune des distributions,
et de sélectionner les contraintes les plus fortes. Ainsi, chacune des distributions sera
respectée. En distribuant la somme dans chacune des inéquations, on obtient alors :

Posons quelques notations, afin d'allèger l'écriture des bornes :


La résolution de ces inéquations pour chaque paramètre nous donne donc :

La fusion de ces contraintes, établies pour chacun des paramètres à optimiser, donne donc finalement les contraintes portant sur le paramètre additionnel. On peut remarquer que, dans tous les cas, la valeur nulle est acceptable. Cela implique donc que, au pire, la descente selon cette direction conduira à une modification nulle des paramètres.
Voici finalement une petite Applet (Java 1.4) permettant de simuler cette méthode de relaxation. La
fonction à optimiser dispose d'une distribution de 3 probabilités, et est
générée aléatoirement. Les deux premières courbes montrent la valeur de
la fonction pour différentes valeurs des deux premiers paramètres. La troisième montre
la valeur de la fonction pour la direction donnée par les modifications des deux courbes
supérieures (le paramètre  ). Le
bouton Nouveau Cycle permet de terminer un cycle d'optimisation, de mémoriser les
valeurs des paramètres. Après, un nouveau cycle peut recommencer.
). Le
bouton Nouveau Cycle permet de terminer un cycle d'optimisation, de mémoriser les
valeurs des paramètres. Après, un nouveau cycle peut recommencer.
Afin de simuler fidèlement l'algorithme, vous devez donc :